Monotonic Stack

---

Monotonic Sequence

• aka: monotonic stack or monotonic queue(deque)
• The word "monotonic" means a list or a function is either always increasing, or always decreasing.
  • We can implement monotonic sequence using either stack or queue, but the later gives us more flexibility as it allows removal from front.
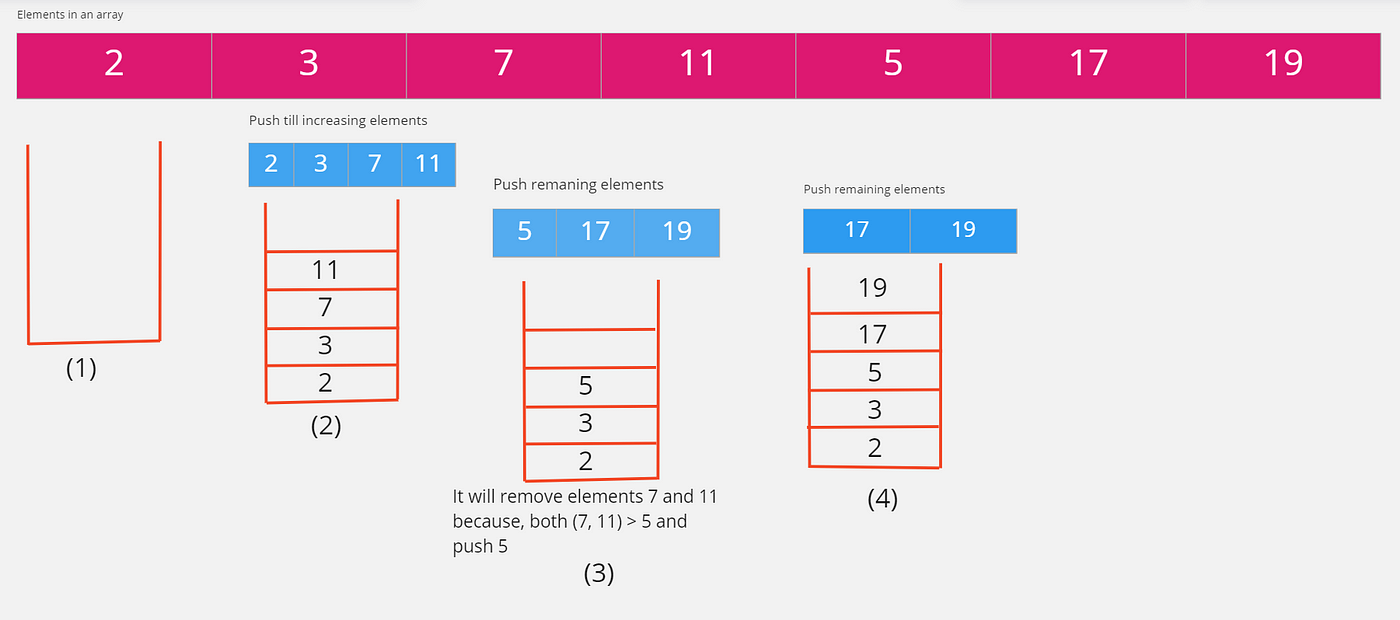
• Monotonic stack is like a regular stack with one key distinction in the push operation:
  • Before we push a new element onto the stack, we first check if adding it breaks the monotonic condition.
  • If it does, then we pop the top element off the stack until pushing the new element no longer breaks the monotonic condition.
• 

Monotonic Sequence Code Template

• To find the next smaller element

# using stack
def mono_stack(nums):
    n = len(nums)
    stack = [] # stores *indices*
    result = [-1] * n
    
    for index in range(n):
        while stack and nums[index] < nums[stack[-1]]: #nums[idx] > ... for next greater elt
            result[stack[-1]] = elt
            stack.pop()
        
        stack.append(index)
    
    return result

#or using queue
def mono_deque(nums):
    n = len(nums)
    deq = deque()
    result = [-1] * n

    for index in range(n):
        while deq and nums[index] < nums[deq[-1]]:
            result[deq[-1]] = nums[index]
            deq.pop()

        deq.append(index)

    return result

Application of Monotonic Stack

• We can use this technique to find the next smaller or greater elt by iterating from start-end
  • Or we can use it to find the previous smaller or greater elt by iterating from end - front
• Next Largest or Smallest Element in a List
  • Get the next greater element for every array element
  • daily-temperatures
  • Trapping Rain Water
  • Largest Rectangle in Histogram
  • Steps to Make Array Non-decreasing
• Maximum or Minimum Element in a Sliding Window

Sliding Window Maximum

• Sliding Window Maximum
  • Find the maximum integer within the window each time it moves.

Input: nums = [1,3,-1,-3,5,3,6,7], k = 3
Output: [3,3,5,5,6,7]
Explanation: 
Window position                Max
---------------               -----
[1  3  -1] -3  5  3  6  7       3
 1 [3  -1  -3] 5  3  6  7       3
 1  3 [-1  -3  5] 3  6  7       5
 1  3  -1 [-3  5  3] 6  7       5
 1  3  -1  -3 [5  3  6] 7       6
 1  3  -1  -3  5 [3  6  7]      7

def sliding_window_maximum(nums: List[int], k: int) -> List[int]:

    q = deque() # stores *indices*
    res = []
    
    for i, cur in enumerate(nums):
        while q and nums[q[-1]] <= cur:
            q.pop() #pop from right/end
        q.append(i)
        
        # if q[0] is out of bound(window size)-> remove it
        if q[0] == i - k:
            q.popleft()

        # if window size == k, (k-1) since we're starting from 0(i=0)
        if i >= k - 1:
            res.append(nums[q[0]])
            
    return res